Опровержение:
|
В той системе отношений, что представлена в предлагаемом парадоксе все стороны квадратов могут быть только четными, так как каждый меньший квадрат, диагональ которого Нх вписана в сторону большего, по площади = 1/2 от большего квадрата и две его площади дадут четную площадь большего квадрата, а четная площадь большего квадрата даст четную его сторону Чx ...
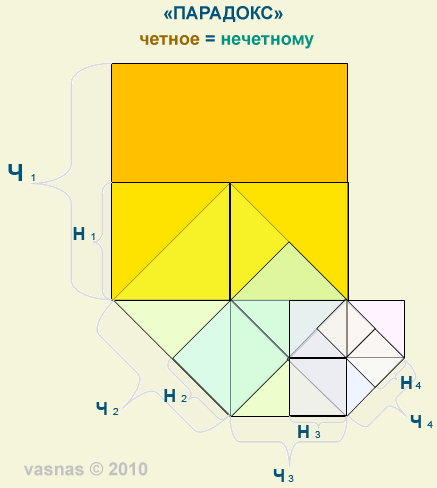
Обманывая парадоксом, нас ведут по ложному пути рассуждений, предлагая сначала предположить, что сторона меньшего квадрата Ч2 нечетна, а большего Ч1 четна и состоит из двух нечетных Н1. Вот тут то и образуется «парадокс»! Получается, что: 2 * Н1 * Н1 = Ч2 * Ч2 , т.е. четное = нечетному ... (?) 2 * Н1 * Н1 = 2 * (неч.) = четное (верно) Ч2 * Ч2 = нечетное * нечетное = нечетное (верно) тогда: четное = нечетное (неверно) Вывод: к парадоксу приводит то, что логике предоставлены отдельные части одной системы, вне системы. См. рисунок: |
 |